聚类分析(英语:Cluster analysis)是对于统计数据分析的一门技术,在许多领域受到广泛应用,包括机器学习,数据挖掘,模式识别,图像分析以及生物信息。聚类是把相似的对象通过静态分类的方法分成不同的组别或者更多的子集(subset),这样让在同一个子集中的成员对象都有相似的一些属性,常见的包括在坐标系中更加短的空间距离等。
定义
聚类就是对大量未知标注的数据集,按数据的内在相似性将数据集划分为多个类别,使类别内的数据相似度较大而类别间的数据相似度较小。显然聚类算法属于无监督学习。
距离度量方式
度量数据间的距离/相似性有一系列不同的方式:
- 闵可夫斯基距离Minkowski/欧式距离: \[dist(X, Y) = (\sum_{i=1}^N(x_i - y_i)^p)^{\frac{1}{p}}\]
- 杰卡德相似系数(Jaccard) : \[J(A, B) = \frac{|A\cap B|}{|A\cup B|}\]
- 余弦相似度(cosine similarity): \[\cos(\theta) = \frac{a^Tb}{|a|\cdot|b|}\]
- Pearson相似系数: \[\rho_{XY} = \frac{cov(X, Y)}{\sigma_X\sigma_Y} = \frac{E[(X - \mu_x)(Y - \mu_y)]}{\sigma_X\sigma_Y} = \frac{\sum_{i=1}^n(x_i - \mu_x)(y_i - \mu_y)}{\sqrt{\sum_{i=1}^n(x_i - \mu_x)^2}\cdot\sqrt{\sum_{i=1}^n(y_i - \mu_y)^2}}\]
- 相对熵(K-L距离): \[D(p || q) = \sum_xp(x)\log\frac{p(x)}{q(x)} = E_{p(x)}\log\frac{p(x)}{q(x)}\]
- Hellinger距离 \[D_\alpha(p||q) = \frac{1}{1-\alpha^2}(1 - \int p(x)^{\frac{1+\alpha}{2}}q(x)^{\frac{1-\alpha}{2}}dx)\]
K-Means
聚类的基本思想
- 给定一个有 \(N\) 个对象的数据集, 构造数据的 \(k\) 个簇, \(k≤n\)。满足下列条件:
- 每一个簇至少包含一个对象
- 每一个对象属于且仅属于一个簇
- 将满足上述条件的 \(k\) 个簇称作一个合理划分,对于给定的类别数目 \(k\), 首先给出初始划分, 通过迭代改变样本和簇的隶属关系, 使得每一次改进之后的划分方案都较前一次好。
K-means算法
K-means算法,也被称为k-平均或k-均值,是一种广泛使用的聚类算法。
- 假定输入样本为 \(S=x_1,x_2,...,x_m\) , 则算法步骤为:
- 选择初始的 \(k\) 个类别中心 \(μ_1, μ_2, ..., μ_k\)
- 对于每个样本 \(x_i\),将其标记为距离类别中心最近的类别, 即: \[label_i = \arg\min_{1\leqslant j \leqslant k}||x_i-\mu_j||\]
- 将每个类别中心更新为隶属该类别的所有样本的均值: \[\mu_j = \frac{1}{c_j}\sum_{i\in c_j}x_i\]
- 重复最后两步,直到类别中心的变化小于某阈值。
- 中止条件:
- 迭代次数/簇中心变化率/最小平方误差MSE(MinimumSquaredError
公式化理解
记 \(K\)个簇中心为 \(\mu_1,\mu_2,...,\mu_k\) , 每个簇的样本数目为\(N_1,N_2,...,N_k\)。 假设使用平方误差作为目标函数: \[J(\mu_1, ... \mu_k) = \frac{1}{2}\sum_{j=1}^K\sum_{i=1}^{N_j}(x_i - \mu_j)^2\]
对它求偏导并令其等于零得:
\[\frac{\partial J}{\partial \mu_j} = -\sum_{i=1}^{N_j}(x_i - \mu_j) = 0 \Rightarrow \mu_j = \frac{1}{N_j}\sum_{i=1}^{N_j}x_i\]
正好和K-mean算法中的聚类中心更新规则相同,即每个类别中心更新为隶属该类别的所有样本的均值,。所以实际上K-mean算法的损失函数就是上面的均方误差损失,更新规则也是梯度下降,而均方误差损失是假设误差服从高斯分布(推导见此处)!也就是说,K-mean算法是假设每个簇的误差是服从正态分布的,虽然这个先验条件很强,但如果实际情况不是这样,K-mean算法也可能给出很好的聚类结果。
K-means算法还对异常点和初始值比较敏感
若簇中含有异常点,将导致均值偏离严重。以一维数据为例 : 数组 \(1, 2, 3, 4, 100\) 的均值为 \(22\),显然离大多数数据都比较远,若改成求数组的中位数 \(3\),在该实例中更为稳妥。这种聚类方式即K-Mediods聚类(K中值聚类),相当于把损失函数换成了绝对误差损失。
若类中心初始值不同,K-means算法可能会得到完全不同的结果(可能是不好的),比如下图所示:

总结
- 优点
- 是解决聚类问题的一种经典算法,简单、快速
- 对处理大数据集,该算法保持可伸缩性和高效率
- 当簇近似为高斯分布时,它的效果较好
- 可作为其他聚类方法的基础算法,如谱聚类
- 缺点
- 在簇的平均值可被定义的情况下才能使用,可能不适用于某些应用
- 必须事先给出 \(k\) (要生成的簇的数目),而且对初值敏感, 对于不同的初始值,可能会导致不同结果
- 不适合于发现非凸形状的簇或者大小差别很大的簇
- 对躁声和孤立点数据敏感
密度聚类
密度聚类方法的指导思想是,只要样本点的密度大于某阈值,则将该样本添加到最近的簇中。
这类算法能克服基于距离的算法只能发现“类圆形”(凸)的聚类的缺点,可发现任意形状的簇, 且对噪声数据不敏感。但计算密度单元的计算复杂度大,需要建立空间索引来降低计算量。常用密度聚类的算法有: * DBSCAN * 密度最大值算法
DBSCAN
Density-Based Spatial Clustering of Applications with Noise
它是一个比较有代表性的基于密度的聚类算法。 与划分和层次聚类方法不同,它将簇定义为密度相连的点的最大集合,能够把具有足够高密度的区域划分为簇,并可在有“噪声” 的数据中发现任意形状的聚类。
先来介绍一些相关概念:
- 对象的 \(ε\)-邻域 : 给定对象在半径 \(ε\) 内的区域
- 核心对象 : 对于给定的数目 \(m\), 如果一个对象的 \(ε\)- 邻域至少包含 \(m\) 个对象, 则称该对象为核心对象
- 直接密度可达 : 给定一个对象集合 \(D\), 如果 \(p\) 是在 \(q\) 的 \(ε\)-邻域内, 而 \(q\) 是一个核心对象, 我们说对象 \(p\) 从对象 \(q\) 出发是直接密度可达的
如右图 \(ε=1\)cm, \(m=5\),  \(q\)是一个核心对象, 从对象 \(q\) 出发到对象 \(p\) 是直接密度可达的。
\(q\)是一个核心对象, 从对象 \(q\) 出发到对象 \(p\) 是直接密度可达的。
密度可达 : 如果存在一个对象链 \(p_1p_2...p_n,p_1=q,p_n=p\), 对 \(p_i∈D\), \((1≤i ≤n)\), \(p_{i+1}\) 是从 \(p_i\) 关于 \(ε\) 和 \(m\) 直接密度可达的, 则对象 \(p\) 是从对象 \(q\) 关于 \(ε\) 和 \(m\) 密度可达的。如下图:

- 密度相连 : 如果对象集合 \(D\) 中存在一个对象 \(o\), 使得对象 \(p\) 和 \(q\) 是从 \(o\) 关于 \(ε\) 和 \(m\) 密度可达的, 那么对象 \(p\) 和 \(q\) 是关于 \(ε\) 和 \(m\) 密度相连的。如下图:
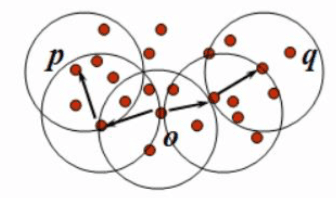
- 簇 : 一个基于密度的簇是最大的密度相连对象的集合
噪声 : 不包含在任何簇中的对象称为噪声
DBSCAN算法流程
- 如果一个点 \(p\) 的 \(ε\)-邻域包含多于 \(m\) 个对象, 则创建一个 \(p\) 作为核心对象的新簇
- 寻找并合并核心对象直接密度可达的对象
- 没有新点可以更新簇时, 算法结束

由该过程我们可以知道: * 每个簇至少包含一个核心对象 * 非核心对象可以是簇的一部分, 构成了簇的边缘(edge) * 包含过少对象的簇被认为是噪声
密度最大值聚类
密度最大值聚类是一种简洁优美的聚类算法,可以识别各种形状的类簇,并且参数很容易确定。
一些定义
- 局部密度 \(\rho_i = \sum_j\chi(d_{ij} - d_c)\),其中 \(\chi(x) = 1, \ if\ x < 0, \ otherwise \ \chi(x) = 0\),\(d_c\) 是一个截断距离,\(ρ_i\) 即到对象 \(i\) 的距离小于 \(d_c\) 的对象的个 数。由于该算法只对 \(ρ_i\) 的相对值敏感, 所以对 \(d_c\) 的选择是稳健的, 一种推荐做法是选择 \(d_c\), 使得平均每个点的邻居数为所有点的 1%-2%
- 高局部密度点距离 \(\delta_i = \min_{j:\rho_j > \rho_i}(d_{ij})\)
- 简称:高密距离
- 在密度高于对象 \(i\) 的所有对象中, 到对象 \(i\) 最近的距离, 即高局部密度点距离
- 对于密度最大的对象, 设置 \(δ_i=\max(d_{ij})\) (即 : 该问题中的无穷大)
- 只有那些密度是局部或者全局最大的点才会有远大于正常值的高局部密度点距离
- 簇的中心:那些有着比较大的局部密度 \(ρ_i\) 和很大的高密距离 \(δ_i\) 的点被认为是簇的中心
- 确定簇中心之后, 其他点按照距离已知簇的中心最近进行分类
- 异常点:高密距离 \(δ_i\) 较大但局部密度 \(ρ_i\) 较小的点是异常点
密度最大值聚类过程
下左图是所有点在二维空间的分布, 下右图是以 \(ρ\) 为横坐标, 以 \(δ\) 为纵坐标绘制的决策图。可以看到, \(1\)和 \(10\) 两个点的 \(ρ_i\) 和 \(δ_i\) 都比较大, 作为簇的中心点。\(26\)、 \(27\)、\(28\)三个点的 \(δ_i\) 也比较大, 但是 \(ρ_i\) 较小, 所以是异常点。

边界和噪声的重认识
在聚类分析中,通常需要确定每个点划分给某个簇的可靠性:
- 在该算法中,可以首先为每个簇定义一个边界区域 (border region),亦即划分给该簇但是距离其他簇的点的距离小于 \(d_c\) 的点的集合。然后为每个簇找到其边界区域的局部密度最大的点,令其局部密度为 \(ρ_h\)。
- 该簇中所有局部密度大于 \(ρ_h\) 的点被认为是簇核心的一 部分(亦即将该点划分给该类簇的可靠性很大),其余的点被认为是该类簇的光晕(halo),亦即可以认为是噪声。
谱聚类
基础知识
特征值和特征向量
若数 \(\lambda\) 和向量 \(\overrightarrow{u}\) 对矩阵 \(A\) 满足: \[A\cdot \overrightarrow{u}= \lambda \cdot \overrightarrow{u} \] 则 \(\lambda\) 称为矩阵 \(A\) 的一个特征值,\(\overrightarrow{u}\) 为对应的特征向量。
则有以下结论: * 实对称阵的特征值是实数 * 证明略 * 实对称阵不同特征值的特征向量正交 * 证明:令实对称矩阵为 \(A\), 其两个不同的特征值 \(λ_1,λ_2\) 对应的特征向量分别是 \(μ_1, μ_2\); * \(λ_1,λ_2,μ_1,μ_2\) 都是实数或是实向量 * 有 \(A\mu_1 = \lambda_1\mu_1\),从而: \[\begin{array}{lcr} \ \ \ \ \ A\mu_2 = \lambda_2\mu_2 \\ \Rightarrow \mu_1^T A\mu_2 = \mu_1^T\lambda_2\mu_2 \\ \Rightarrow (A^T\mu_1)^T\mu_2 = \lambda_2\mu_1^T\mu_2 \\ \Rightarrow (A\mu_1)^T\mu_2 = \lambda_2\mu_1^T\mu_2 \\ \Rightarrow (\lambda_1\mu_1)^T\mu_2 = \lambda_2\mu_1^T\mu_2 \\ \Rightarrow \lambda_1\mu_1^T\mu_2 = \lambda_2\mu_1^T\mu_2 \\ \end{array}\] * 因为 \(\lambda_1 \neq \lambda_2\),所以 \(\mu_1^T\mu_2 = 0\),即 \(\mu_1,\mu_2\) 正交。
谱和谱聚类
- 谱:方阵作为线性算子,它的所有特征值的全体统称方阵的谱。
- 我们说一个人靠不靠谱儿,实际上是看他以前做过的事的稳定程度,即方差。
- 方阵的谱半径为最大的特征值
- 普通矩阵 \(A\) 的谱半径: \((A^TA)\) 的最大特征值
谱聚类是一种基于图论的聚类方法, 通过对样本数据的拉普拉斯矩阵的特征向量进行聚类, 从而达到对样本数据聚类的目的。
谱分析的整体过程
给定一组数据 \(x_1,x_2,...x_n\), 记任意两个点之间的相似度(“距离”的减函数)为\(s_{ij}=<x_i,x_j>\), 形成相似度图(similarity graph) : \(G=(V,E)\) 。如果 \(x_i\) 和 \(x_j\) 之间的相似度 \(s_{ij}\) 大于一定的阈值, 那么两个点是连接的, 权值记做 \(s_{ij}\)。
接下来, 可以用相似度图来解决样本数据的聚类问题 : 找到图的一个划分, 形成若干个组(Group), 使得不同组之间有较低的权值, 组内有较高的权值。
一些概念
- 邻接矩阵 \(W = (w_{ij})\ \ i,j=1,...n\),实际上该矩阵就是相似度矩阵,即 \(w_{ij} = s_{ij}\)
- 度矩阵 \(D = (d_{i})\ \ i = 1,...,n\),该矩阵是个对角阵: \[d_i = \sum_{j=1}^nw_{ij}\]
- 高斯相似度 \(s(x_i, x_j) = \exp(\frac{-||x_i - x_j||^2}{2\sigma^2})\)
- Laplace矩阵:\(L = D - W\)
- \(L\) 是对称半正定矩阵,最小特征值是 \(0\),相应的特征向量是全 \(1\) 向量 \[\begin{array}{lcr} f^TLf = f^TDf - f^TWf = \sum_{i=1}^nd_if_i^2 - \sum_{i,j=1}^nf_if_jw_{ij} \\ = \frac{1}{2}( \sum_{i=1}^nd_if_i^2 - 2\sum_{i,j=1}^nf_if_jw_{ij} + \sum_{j=1}^nd_jf_j^2) \\ = \frac{1}{2}\sum_{i,j=1}^nw_{ij}(f_i-f_j)^2 \geqslant 0 \end{array}\]
- 其中,\(f\) 为任意矩阵,所以 \(L\) 为半正定矩阵。
- Laplace 矩阵的其它形式:
- 对称Laplace矩阵 \(L_{sym} = D^{-\frac{1}{2}}LD^{\frac{1}{2}} = I - D^{-\frac{1}{2}}WD^{\frac{1}{2}}\)
- 随机游走Laplace矩阵 \(L_{rw} = D^{-1}L = I - D^{-1}W\)
- 之所以叫 Random Walk 是因为 \(d_i = \sum_{j=1}^nw_{ij}\),\(D^{-1}W\) 相当于 \(W\) 的元素都变成了 \(\frac{w_{ij}}{d_i} = \frac{w_{ij}}{\sum_{j=1}^nw_{ij}}\),相当于做了归一化。如果令 \(P = D^{-1}W\),则 \(\sum_{j=1}^np_{ij} = 1\),\(p_{ij}\) 就可以看成从点 \(i\) 到 \(j\) 的概率,也就是 Random Walk 模型了。
谱聚类算法
- 输入: \(n\) 个点 \(\{p_i\}\), 簇的数目 \(k\)
- 计算 \(n×n\) 的相似度矩阵 \(W\) 和度矩阵 \(D\);
- 计算拉普拉斯矩阵 \(L=D-W\);
- 计算 \(L\) 的前 \(k\) 个特征向量 \(u_1,u_2,...,u_k\)(从小到大排列);
- 将 \(k\) 个列向量 \(u_1,u_2,...,u_k\) 组成矩阵 \(U\), \(U∈R^{n×k}\);
- 对于 \(i=1,2,...,n\), 令 \(y_i∈R^k\) 是 \(U\) 的第 \(i\) 行的向量;
- 使用k-means算法将点 \((y_i)_{i=1,2,...,n}\) 聚类成簇 \(C_1,C_2,...C_k\);
- 输出簇 \(A_1,A_2,...A_k\), 其中, \(A_i=\{j\ |\ y_j∈C_i\}\)
使用其它形式的Laplace矩阵算法步骤类似。
由于最后聚类的过程实际上还是交给k-means来做,所以谱聚类前面所有过程可以看作是给k-means提供更好的特征。
谱聚类与PCA的联系
谱聚类中取Laplace矩阵 \(L\) 从小到大的前 \(k\) 特征向量,相当于把数据从 \(n\) 为降低到 \(k\) 维,就是一个降维的过程,与PCA是类似的。PCA是取原始数据的协方差矩阵的前 \(k\) 个特征向量,只不过是从大到小排列的。为什么会有顺序区别呢?原因是Laplace矩阵 \(L = D - W\) 中的减号,也就是 \(L\) 中的特征与原始数据(\(W\))的特征是相反的,所以与PCA取的顺序相反。
思考与总结
- 谱聚类中的 \(K\) 如何确定 ?
- \(k^* = \arg\max_k|\lambda_{k+1} - \lambda_k|\)
- 最后一步K-Means的作用是什么 ?
- 目标函数是关于子图划分指示向量的函数,该向量的值根据子图划分确定,是离散的。该问题是NP的,转换成求连续实数域上的解,最后用K-Means算法离散化。
- 未正则/对称/随机游走拉普拉斯矩阵,首选哪个?
- 随机游走拉普拉斯矩阵
- 谱聚类可以用切割图/随机游走/扰动论等解释
参考
- Alex Rodriguez, Alessandro Laio. Clustering by fast search and find of density peak. Science. 2014
- Ulrike von Luxburg. A tutorial on spectral clustering. 2007
- Lang K. Fixing two weaknesses of the spectral method. Advances in Neural Information Processing Systems 18, 715–722. MIT Press, Cambridge, 2006
- Bach F, Jordan M. Learning spectral clustering. Advances in Neural Information Processing Systems 16 (NIPS). 305– 312. MIT Press, Cambridge,2004
- Andrew Rosenberg, Julia Hirschberg, V-Measure: A conditional entropy-based external cluster evaluation measure, 2007.
- W. M. Rand. Objective criteria for the evaluation of clustering methods. Journal of the American Statistical Association. 1971
- Nguyen Xuan Vinh, Julien Epps, James Bailey, Information theoretic measures for clusterings comparison, ICML 2009
- Peter J. Rousseeuw, Silhouettes: a Graphical Aid to the Interpretation and Validation of Cluster Analysis. Computational and Applied Mathematics 20: 53–65, 1987