NIUHE

日々私たちが过ごしている日常というのは、実は奇迹の连続なのかもしれんな

PyTorch源码浅析(3)：NN

THNN是一个用C语言实现的神经网络模块的库，提供的功能非常底层。它实现了许多基础的神经网络模块，包括线性层，卷积层，Sigmoid等各种激活层，一些基本的loss函数，这些API都声明在THNN/generic/THNN.h中。每个模块都实现了前向传导（forward）和后向传导（backward）的功能。THCUNN则是对应模块的CUDA实现。

目录

THNN & THCUNN

我们通过几个例子具体看一下几种模块是怎么实现的。

Tanh

首先从最简单的激活层开始看，以 \(\tanh​\) 为代表，代码在THNN/generic/Tanh.c。这个模块只有两个函数，分别是THNN_(Tanh_updateOutput)()和THNN_(Tanh_updateGradInput)()，其中前者实现了前向传播，后者实现了反向传播。注意到函数的命名方式，依旧是使用宏实现范式，THNN_是宏定义，Tanh_是具体模块名，updateOutput表示前向传播，updateGradInput表示反向传播，与之前不同的是，这里只需生成浮点类型（float和double）的实现即可。

前向传播的实现很简单，直接调用之前实现的tanh函数就行了：

1
2
3
4
5
6
7
void THNN_(Tanh_updateOutput)(
          THNNState *state,
          THTensor *input,
          THTensor *output)
{
  THTensor_(tanh)(output, input);
}

它有三个参数，分别是THNN状态（暂不知有何用），本层的输入（input）和本层的输出（output），输出存储在output参数中。

反向传播的实现为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
void THNN_(Tanh_updateGradInput)(
          THNNState *state,
          THTensor *gradOutput,
          THTensor *gradInput,
          THTensor *output)
{
  THNN_CHECK_SHAPE(output, gradOutput);
  THTensor_(resizeAs)(gradInput, output);

  if (/* output, gradInput, 和 gradOutput 的内存是连续的 */)
  {
    TH_TENSOR_APPLY3(scalar_t, gradInput, scalar_t, gradOutput,
                     scalar_t, output,
      scalar_t z = *output_data;            \
      *gradInput_data = *gradOutput_data * (1. - z*z);
    );
  }
  else
  {
    scalar_t* ptr_gradOutput = gradOutput->data<scalar_t>();
    scalar_t* ptr_gradInput  = gradInput->data<scalar_t>();
    scalar_t* ptr_output     = output->data<scalar_t>();
    int64_t i;

#pragma omp parallel for private(i)
    for (i = 0; i < THTensor_(nElement)(gradInput); i++)
    {
      scalar_t z = ptr_output[i];
      ptr_gradInput[i] = ptr_gradOutput[i] * (1. - z*z);
    }
  }
}

反向传播接收5个参数，分别是THNN状态，从后面传回来的梯度（gradOutput），本层往回传的梯度（gradInput），本层前向传播的输出（output），这个函数计算的是本层的梯度，然后存储在gradInput中。

\(\tanh\) 的导数为： \[ f(z) = \tanh(z)\\ f'(z) = 1 - (f(z))^2 \] 其中，\(f(z)​\) 就是前向传播时本层的输出，也就是output参数（循环里的z），根据链式法则，再乘以后面层传回来的梯度（gradOutput）就是本层应该往回传的梯度了（相对于本层输入的梯度），所以循环里的代码为：

1
*gradInput_data = *gradOutput_data * (1. - z*z);

注：_data后缀表示数据指针，具体可以看Apply宏的实现。

2D Convolution

最普通的2D卷积，CPU实现在THNN/generic/SpatialConvolutionMM.c，CUDA实现在THCUNN/generic/SpatialConvolutionMM.cu，大体的算法是把输入展开成一个特殊的矩阵，然后把卷积转化为矩阵相乘（MM = Matrix Multiplication）。模块里主要包含三个函数，前向传播（THNN_(SpatialConvolutionMM_updateOutput)()），反向传播（THNN_(SpatialConvolutionMM_updateGradInput)()），和更新层内参数（THNN_(SpatialConvolutionMM_accGradParameters)()）。

前向传播

PyTorch实现卷积的做法是用im2col算法把输入展开成一个大矩阵，然后用kernel乘以这个大矩阵，就得了卷积的结果。这里不具体介绍im2col算法是怎么做的，但会解释为什么可以这么做。

首先定义符号，为了和代码中的符号一致，首先来看一下updateOutput的声明：

1
2
3
4
5
6
7
8
9
10
11
void THNN_(SpatialConvolutionMM_updateOutput)(
           THCState *state,
           THCTensor *input,
           THCTensor *output,
           THCTensor *weight,
           THCTensor *bias,
           THCTensor *columns,
           THCTensor *ones,
           int kW, int kH,
           int dW, int dH,
           int padW, int padH);

其中，

  • input是输入的4D Tensor，大小为 \(\text{batch}\times\text{nInputPlane}\times\text{inputHeight}\times\text{inputWidth}\)，batch维也可以没有，就变为3D Tensor；
  • output是输出的4D或3D Tensor，大小为 \(\text{batch}\times\text{nOutputPlane}\times\text{outputHeight}\times\text{outputWidth}\)，其中，

\[ \text{outputHeight}=\frac{\text{inputHeight}+2\ast\text{padH}-\text{kH}}{\text{dH}}+1\\ \text{outputWidth}=\frac{\text{inputWidth}+2\ast\text{padW}-\text{kW}}{\text{dW}}+1 \]

  • weight是权重，也就是卷积核，大小为 \(\text{nOutputPlane}\times\text{nInputPlane}\times\text{kH}\times\text{kW}\)；
  • bias是偏置，大小为 \(\text{nOutputPlane}\times1\times1\times1\)；
  • columns用于存储im2col的结果；
  • ones是一个值全为1的矩阵，大小为 \(\text{outputHeight}\times\text{outputWidth}\)，用于计算偏置；
  • kW和kH是卷积核（kernel）的宽和高；
  • dW和dH是步长（stride）；
  • padW和padH是补零的宽和高。

定义好了符号之后来看一下卷积是怎么转化为一个矩阵乘法的。首先来看卷积是怎么做的，下图是一个简单的例子，其中输入和输出深度 \(\text{nInputPlane}=\text{nOutputPlane}=1​\)，卷积核大小 \(\text{kH}=\text{kW}=3​\)，输入大小 \(\text{inputHeight}=\text{inputWidth}=7​\)，步长 \(\text{dW}=\text{dH}=2​\)，补零 \(\text{padW}=\text{padH}=1​\)，可以算出 \(\text{outputHeight}=\text{outputWidth}=3​\)。

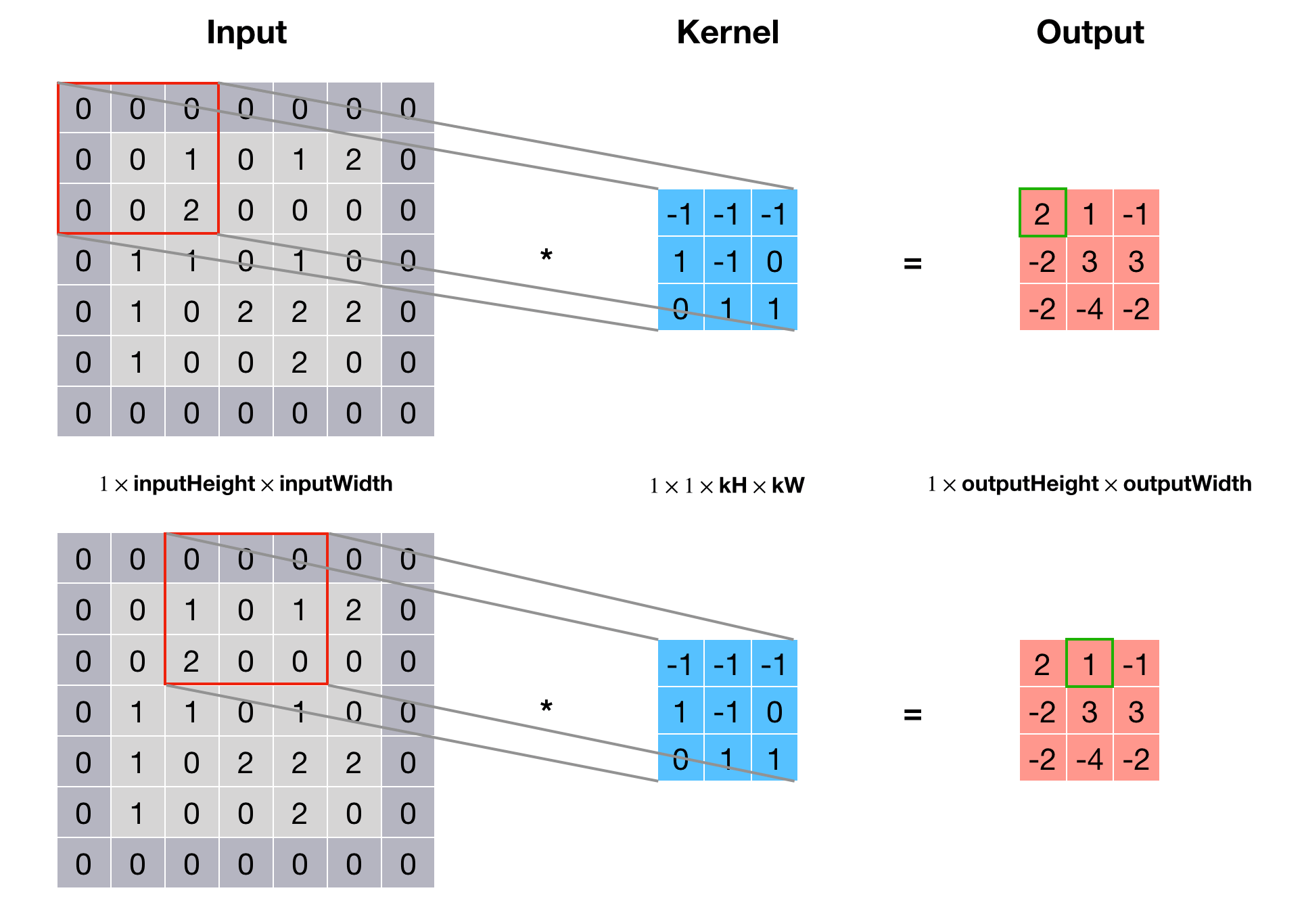
要想把卷积变成一次矩阵乘法运算，就需要把输入中每个卷积窗口变为单独一列，这也就是im2col做的事情，见下图：

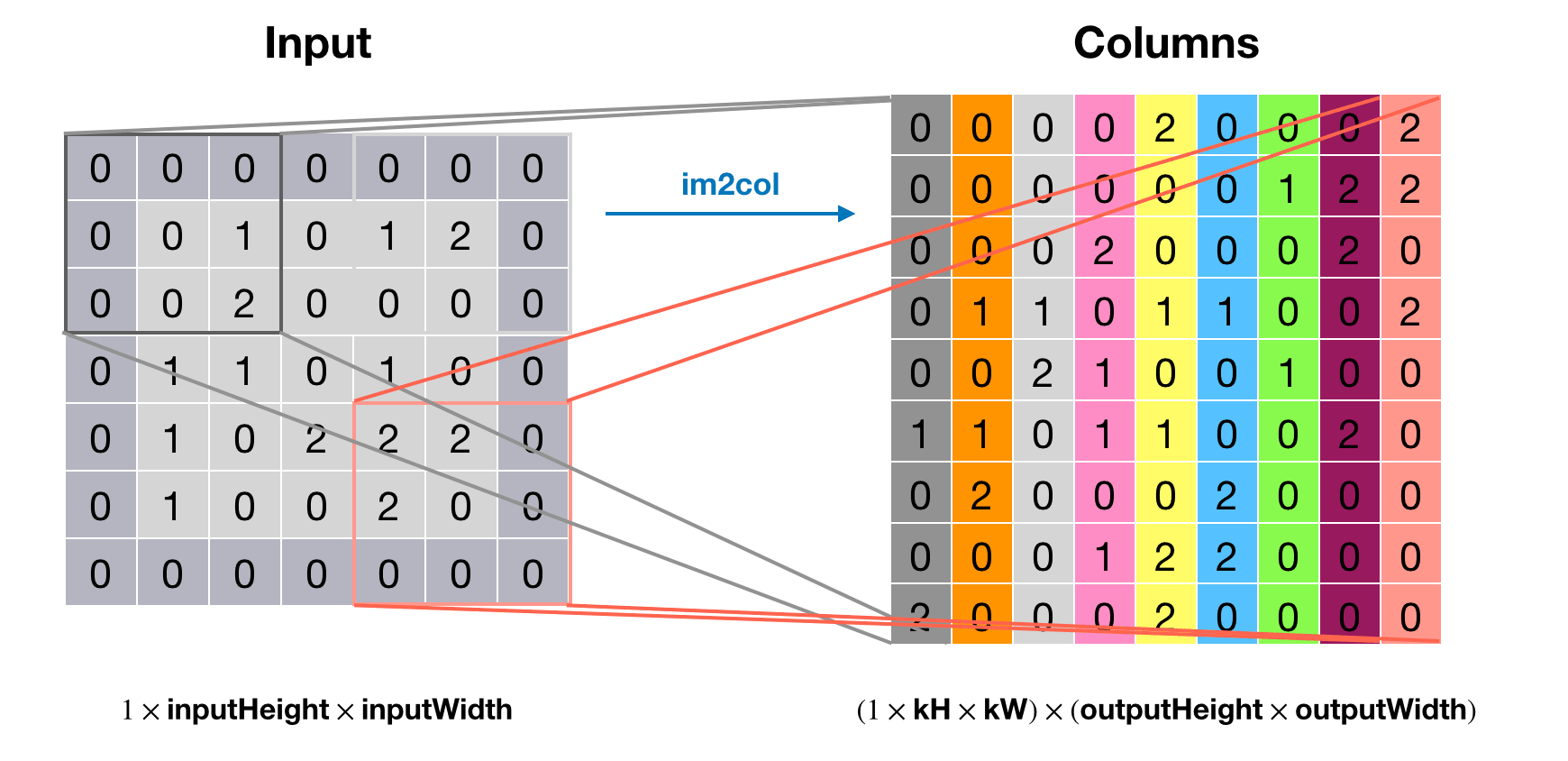
上图中右边矩阵的每一列都是原输入矩阵的一个卷积窗口，转换后的矩阵大小为 \[ (\text{nInputPlane}\times\text{kH}\times\text{kW})\times(\text{outputHeight}\times\text{outputWidth}) \] 得到上述矩阵之后，只需把kernel的大小也resize成 \[ (\text{nOutputPlane})\times(\text{nInputPlane}\times\text{kH}\times\text{kW}) \] 就可以直接用kernel乘以该矩阵得到卷积结果了，见下图。

代码（CUDA版）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
void THNN_(SpatialConvolutionMM_updateOutput)(/* 参数列表前面有 */) {
  /* 省略了一些常规check */
  
  /* resize 卷积核 */
  weight = THNN_(newViewWeightMM2d)(state, weight);
  /* 对输入的维度进行check */
  THNN_(SpatialConvolutionMM_shapeCheck)
       (state, input, NULL, weight, bias, kH, kW, dH, dW, padH, 
        padW, 0);

  int ndim = input->dim();
  int dimf = 0;
  int dimh = 1;
  int dimw = 2;

  if (ndim == 4) {	/* 如果输入是4D的话，第0维是batch size */
    dimf++;
    dimh++;
    dimw++;
  }

  /* 计算输入输出大小 */
  int64_t nInputPlane = input->size(dimf);
  int64_t inputHeight  = input->size(dimh);
  int64_t inputWidth   = input->size(dimw);
  int64_t nOutputPlane = weight->size(0);
  int64_t outputHeight = (inputHeight + 2*padH - kH) / dH + 1;
  int64_t outputWidth  = (inputWidth + 2*padW - kW) / dW + 1;

	
  input = THCTensor_(newContiguous)(state, input);
  int is_batch = 1;
  if (input->dim() == 3) {
    /* 强行加入 batch 维度，把输入变为4D Tensor（batch size = 1）*/
    is_batch = 0;
    THCTensor_(resize4d)(state, input, 1, input->size(0), 
                         input->size(1), input->size(2));
  }

  /* 获取 batch size */
  int64_t batchSize = input->size(0);

  // Resize output
  THCTensor_(resize4d)(state, output, batchSize, nOutputPlane,
                       outputHeight, outputWidth);

  /* Resize columns 矩阵 */
  THCTensor_(resize2d)(state, columns, nInputPlane*kW*kH,
                       outputHeight*outputWidth);

  /* 定义 buffer `ones`，代码略 */

  // Helpers
  THCTensor *input_n = THCTensor_(new)(state);
  THCTensor *output_n = THCTensor_(new)(state);

  /* 对每个batch单独计算： */
  for (int elt = 0; elt < batchSize; elt ++) {
    /* 取出对应batch的输入和输出buffer */
    /* input_n = input[elt] */
    THCTensor_(select)(state, input_n, input, 0, elt);
    THCTensor_(select)(state, output_n, output, 0, elt);

    /* 首先计算偏置 bias，即把 bias 存到 output_n 中 */
    // M,N,K are dims of matrix A and B
    int64_t m_ = nOutputPlane;
    int64_t n_ = outputHeight * outputWidth;
    int64_t k_ = 1;

    /* 调用 GEMM 计算 output_n = 1 * ones * bias + 0 * output_n */
    if (bias) {
      #ifdef THC_REAL_IS_FLOAT
      THCudaBlas_Sgemm(
      #elif defined(THC_REAL_IS_HALF)
      THCudaBlas_Hgemm(
      #elif defined(THC_REAL_IS_DOUBLE)
      THCudaBlas_Dgemm(
      #endif
          state,
          't', 'n',
          n_, m_, k_,
          ScalarConvert<int, scalar_t>::to(1),
          THCTensor_(data)(state, ones), k_,
          THCTensor_(data)(state, bias), k_,
          ScalarConvert<int, scalar_t>::to(0),
          THCTensor_(data)(state, output_n), n_
      );
    } else {
      /* 如果没有 bias 就把 output_n 填零 */
      THCTensor_(zero)(state, output_n);
    }

    /* 用 im2col 把输入 input_n 转化为列矩阵存储在 columns */
    im2col(
      THCState_getCurrentStream(state),
      THCTensor_(data)(state, input_n),
      nInputPlane, inputHeight, inputWidth,
      outputHeight, outputWidth,
      kH, kW, padH, padW, dH, dW,
      1, 1, THCTensor_(data)(state, columns)
    );

    /* 接下来计算 kernel * columns: */
    int64_t m = nOutputPlane;
    int64_t n = columns->size(1);
    int64_t k = nInputPlane*kH*kW;

    /* 计算 output_n = 1 * weight * columns + 1 * bias */
    /* 代码中 columns 在 weight 前面是因为 GEMM 假设矩阵是列主序 */
    #ifdef THC_REAL_IS_FLOAT
    THCudaBlas_Sgemm(
    #elif defined(THC_REAL_IS_HALF)
    THCudaBlas_Hgemm(
    #elif defined(THC_REAL_IS_DOUBLE)
    THCudaBlas_Dgemm(
    #endif
        state,
        'n', 'n',
        n, m, k,
        ScalarConvert<int, scalar_t>::to(1),
        THCTensor_(data)(state, columns), n,
        THCTensor_(data)(state, weight), k,
        ScalarConvert<int, scalar_t>::to(1),
        THCTensor_(data)(state, output_n), n
    );
  }

  /* free 临时变量 input_n, output_n 等 */
  /* resize 输出矩阵，代码略 */
}

反向传播

首先来看一下卷积层反向传播的公式，设第 \(l\) 层的输入为 \(a^{l-1}\)，卷积核为 \(W\)，偏置为 \(b\)，输出为 \(z^l = a^{l-1}*W+b\)，相对于输出的误差梯度为 \(\delta^l = \frac{\partial \text{Loss}}{\partial z^l}\)，则相对于输入的梯度为： \[ \delta^{l-1}=\delta^l*\text{rot180}(W^l) \] 相对于权重和偏置的梯度为： \[ \frac{\partial\text{Loss}}{\partial W^l}=\frac{\partial\text{Loss}}{\partial z^l}\frac{\partial z^l}{\partial W^l}=a^{l-1}*\delta^l\\ \frac{\partial\text{Loss}}{\partial b^l}=\sum_{u,v}(\delta^l)_{u,v} \] 注：\(*\) 为卷积的意思，\(\text{rot180}(x)\) 为把矩阵 \(x\) 旋转180度的意思。公式推导可以看这篇博客。

从公式可以看出反向传播分为两个部分：计算对输入的梯度和计算对参数的梯度，这两部分也分别对应了模块里的两个函数，我们一个一个分析。

THNN_(SpatialConvolutionMM_updateGradInput)

这部分是计算对输入的梯度，虽然公式摆在了那里，但Torch的代码实现并不是直接翻译公式，我也一直没能把这部分的实现和公式对上，不过倒是可以通过图示的方式来理解，有点像前向传播的逆过程，把卷积后的梯度分配回卷积前。

在画图之前还是先定义一些符号：

1
2
3
4
5
6
7
8
9
10
11
void THNN_(SpatialConvolutionMM_updateGradInput)(
           THCState *state,
           THCTensor *input,
           THCTensor *gradOutput,
           THCTensor *gradInput,
           THCTensor *weight,
           THCTensor *gradColumns,
           THCTensor *ones,
           int kW, int kH,
           int dW, int dH,
           int padW, int padH);

其中（与前向传播相同的参数就不重复介绍了），

  • gradOutput 是相对于输出的梯度，即 \(\delta^l\)，大小与前向传播的输出 output 相同；
  • gradInput 是相对于输入的梯度，即 \(\delta^{l-1}\)，是这个函数需要计算的对象，大小与输入 input 相同；
  • gradColumns 是个列矩阵，用于存储临时的梯度，大小为 \((\text{nInputPlane}\times\text{kH}\times\text{kW})\times(\text{outputHeight}\times\text{outputWidth})\)；

代码的实现逻辑是用权重的转置乘以输出梯度，得到gradColumns，然后通过col2im还原到输入的大小，即得到了相对输入的梯度 gradInput。这个操作看起来就是前向传播的逆操作，但是搞不懂为什么这样就实现了 \(\delta^l*\text{rot180}(W^l)\)，如果有大佬知道希望评论区指点一下。使用前面例子的设定，这波操作的示意图如下所示：

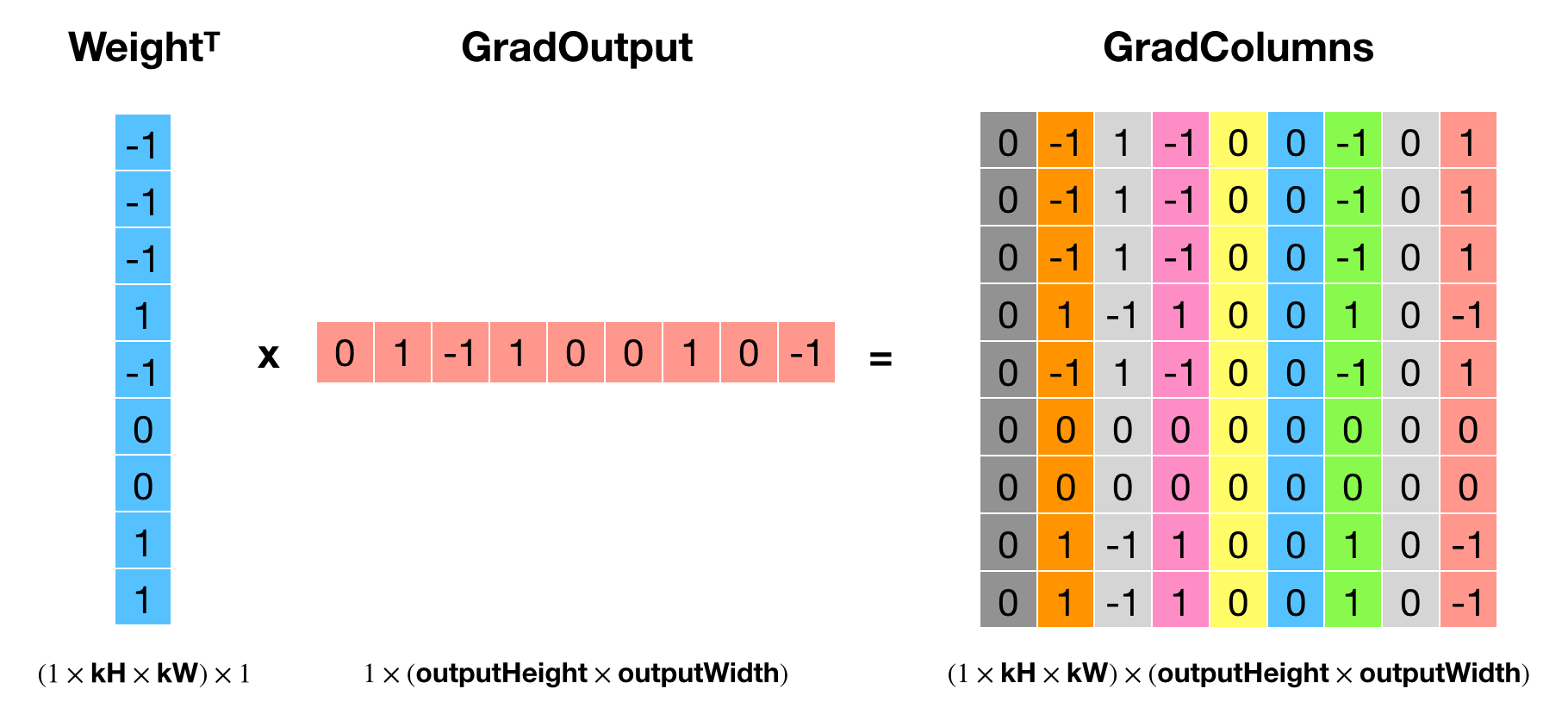
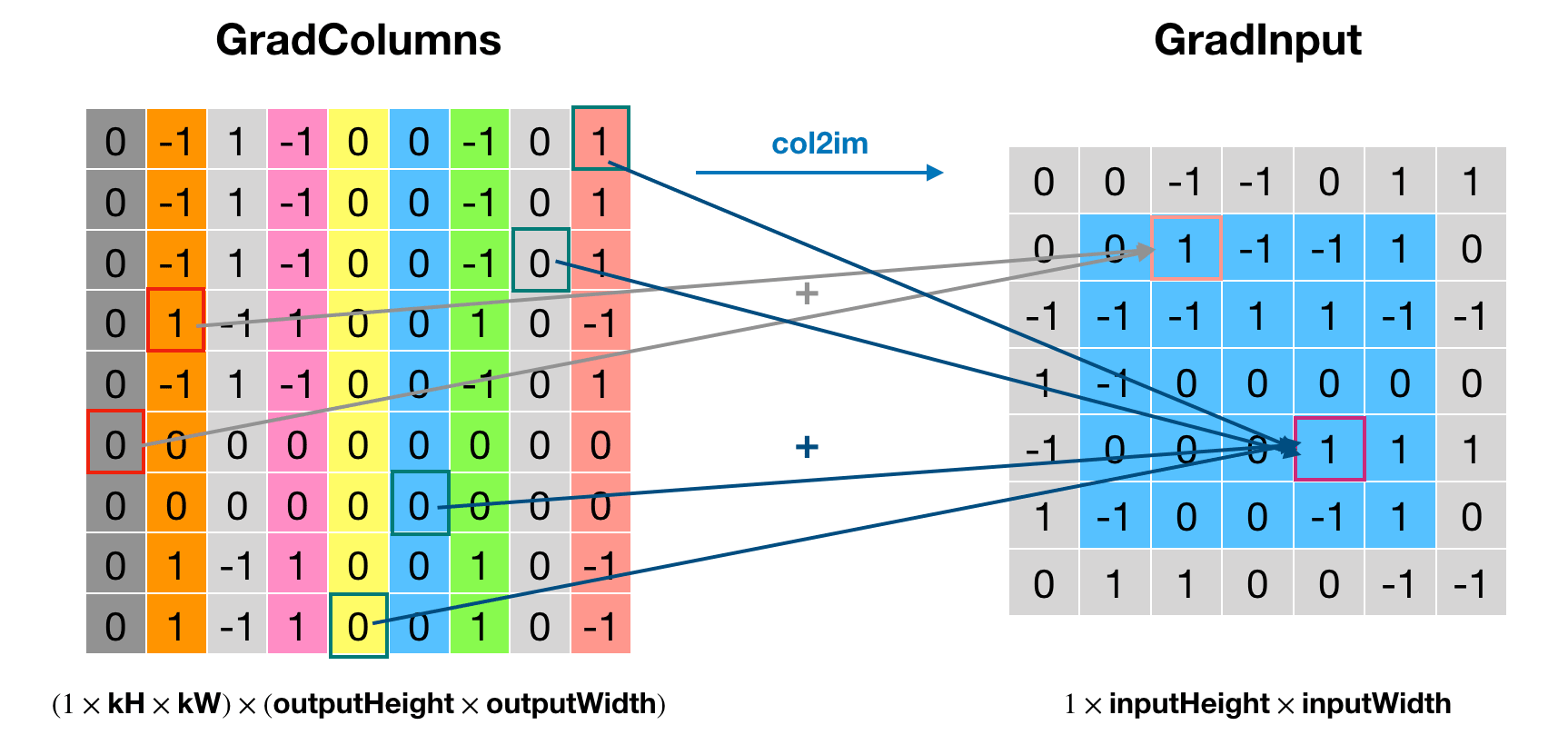
核心部分代码（其余部分与前向传播类似）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/* 循环取每个批次： */
for (int elt = 0; elt < batchSize; elt ++) {
  /* gradInput_n = gradInput[elt]; gradInput_n 同理 */
  THCTensor_(select)(state, gradInput_n, gradInput, 0, elt);
  THCTensor_(select)(state, gradOutput_n, gradOutput, 0, elt);

  // M,N,K are dims of matrix A and B
  int64_t m = nInputPlane*kW*kH;
  int64_t n = gradColumns->size(1);
  int64_t k = nOutputPlane;

  /* 调用GEMM计算 gradColumns = weight' * gradOutput_n */
  #ifdef THC_REAL_IS_FLOAT
  THCudaBlas_Sgemm(
  #elif defined(THC_REAL_IS_HALF)
  THCudaBlas_Hgemm(
  #elif defined(THC_REAL_IS_DOUBLE)
  THCudaBlas_Dgemm(
  #endif
      state,
      'n', 't',
      n, m, k,
      ScalarConvert<int, scalar_t>::to(1),
      THCTensor_(data)(state, gradOutput_n), n,
      THCTensor_(data)(state, weight), m,
      ScalarConvert<int, scalar_t>::to(0),
      THCTensor_(data)(state, gradColumns), n
  );

  /* 调用 col2im 把 gradColumns 还原为 gradInput_n */
  col2im<scalar_t, accreal>(
    THCState_getCurrentStream(state),
    THCTensor_(data)(state, gradColumns),
    nInputPlane, inputHeight, inputWidth, outputHeight,
    outputWidth, kH, kW, padH, padW, dH, dW,
    1, 1, THCTensor_(data)(state, gradInput_n)
  );
}

THNN_(SpatialConvolutionMM_accGradParameters)

接下来看计算参数梯度的部分，这部分相对好理解，因为代码和公式一样，还是先看函数声明：

1
2
3
4
5
6
7
8
9
10
11
12
void THNN_(SpatialConvolutionMM_accGradParameters)(
           THCState *state,
           THCTensor *input,
           THCTensor *gradOutput,
           THCTensor *gradWeight,
           THCTensor *gradBias,
           THCTensor *columns,
           THCTensor *ones,
           int kW, int kH,
           int dW, int dH,
           int padW, int padH,
           accreal scale_);

其中，

  • gradWeight 是权重的梯度，是这个函数需要计算的对象，大小和权重相同；
  • gradBias 是偏置的梯度，也是函数需要计算的对象，大小与偏置相同（就是一个Vector）
  • columns 是用来存储 im2col 的结果，因为要计算卷积，所以要把输入展开
  • scale_ 是学习速率（learning rate）

已知权重梯度的计算公式为 \(\frac{\partial\text{Loss}}{\partial W^l}=a^{l-1}*\delta^l\)，这个卷积的计算方式和前向传播相同：首先把输入（\(a^{l-1}\)）通过im2col展开为列矩阵，存储到columns里，然后用 gradOutput 乘以 columns 计算卷积。而偏置梯度的计算就是把 gradOutput 累加成一个长度为 \(\text{nOutputPlane}​\) 的 Tensor 即可。

核心代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
void THNN_(SpatialConvolutionMM_accGradParameters)(/* 略 */) {
  /* ... */
  
  /* 循环取每个batch： */
  for (int elt = 0; elt < batchSize; elt ++) {
    /* gradOutput_n = gradOutput[elt] */
    THCTensor_(select)(state, gradOutput_n, gradOutput, 0, elt);

    /* 计算权重梯度 */
    if (gradWeight) {
      /* input_n = input[elt] */
      THCTensor_(select)(state, input_n, input, 0, elt);

      /* 把 input_n 展开为 columns */
      im2col(
        THCState_getCurrentStream(state),
        THCTensor_(data)(state, input_n),
        nInputPlane, inputHeight, inputWidth,
        outputHeight, outputWidth,
        kH, kW, padH, padW, dH, dW,
        1, 1, THCTensor_(data)(state, columns)
      );

      
      int64_t m = nOutputPlane;
      int64_t n = nInputPlane*kW*kH;
      int64_t k = columns->size(1);

      /* 调用GEMM计算gradWeight += scale * gradOutput_n * columns'*/
      #ifdef THC_REAL_IS_FLOAT
      THCudaBlas_Sgemm(
      #elif defined(THC_REAL_IS_HALF)
      THCudaBlas_Hgemm(
      #elif defined(THC_REAL_IS_DOUBLE)
      THCudaBlas_Dgemm(
      #endif
          state,
          't', 'n',
          n, m, k,
          scale,
          THCTensor_(data)(state, columns), k,
          THCTensor_(data)(state, gradOutput_n), k,
          ScalarConvert<int, scalar_t>::to(1),
          THCTensor_(data)(state, gradWeight), n
      );
    }

    /* 计算偏置梯度 */
    if (gradBias) {
     	
      int64_t m_ = nOutputPlane;
      int64_t k_ = outputHeight * outputWidth;

      /* 调用GEMV计算 gradBias += scale * gradOutput_n * ones */
      #if defined(THC_REAL_IS_FLOAT) || defined(THC_REAL_IS_DOUBLE)
      #ifdef THC_REAL_IS_FLOAT
      THCudaBlas_Sgemv(
      #elif defined(THC_REAL_IS_DOUBLE)
      THCudaBlas_Dgemv(
      #endif
          state,
          't',
          k_, m_,
          scale,
          THCTensor_(data)(state, gradOutput_n), k_,
          THCTensor_(data)(state, ones), 1,
          ScalarConvert<int, scalar_t>::to(1),
          THCTensor_(data)(state, gradBias), 1
      );
      #endif
      #ifdef THC_REAL_IS_HALF
      THCudaBlas_Hgemm(
          state,
          't', 'n',
          m_, 1, k_,
          scale,
          THCTensor_(data)(state, gradOutput_n), k_,
          THCTensor_(data)(state, ones), k_,
          ScalarConvert<int, scalar_t>::to(1),
          THCTensor_(data)(state, gradBias), m_
      );
      #endif
    }
  }
  
  /* ... */
}

ATen

看了THNN.h的读者可能会发现，THNN和THCUNN只定义了少量的神经网络相关的函数，其实大部分都定义在ATen中，这个ATen是指pytorch/aten/src/ATen文件夹（下同）。说到底，TH系列库都是torch lua时代留下的产物，是用C语言实现的，后来PyTorch开发者觉得cpp大法好，就用C++写了ATen，把TH里的接口都封装了，同时新的API直接在ATen里实现。

这个ATen有点意思，它大概干了这么几件事情：

  • 在ATen/core/Tensor.h定义了at::Tensor类型，这个是C++前端以及更上层的API都在用的Tensor类型，它的成员内有一个TensorImpl impl_，提供底层实现；
  • 实现和封装了有关Tensor的所有操作，并根据数据类型和设备进行自动派发；
  • 使用Python脚本生成ATen API。

其中从TH（包括THC、THNN等）里封装的函数叫做 legacy函数，而在ATen直接实现的函数叫 native函数。native函数的实现全在ATen/native文件夹中，实现了THNN里没有的神经网络和Tensor操作，比如RNN什么的，API列表在ATen/native/native_functions.yaml里，感兴趣的童鞋可以自己阅读。

了解了神经网络每一层的前向传播和反向传播的实现之后，下一步就是控制执行顺序了，也就是自动微分（Autograd），下一章将介绍PyTorch自动微分的实现。

つづく

上一篇：THC 下一篇：Autograd
博客 Neural NetworkPyTorchTHNNCONV

Powered by Hexo and Theme by Hacker
© 2019 NIUHE